What Is the Point Where All Numbers Meet Again

Here we are providing Real Numbers Class 10 Extra Questions Maths Chapter 1 with Answers Solutions, Extra Questions for Class x Maths was designed by subject good teachers.

Extra Questions for Class x Maths Real Numbers with Answers Solutions

Extra Questions for Grade 10 Maths Affiliate i Existent Numbers with Solutions Answers

Real Numbers Form x Extra Questions Very Short Respond Type

Question i.
What is the HCF of the smallest composite number and the smallest prime?
Solution:
Smallest composite number = 4
Smallest prime number = 2
And then, HCF (4, two) = 2

Question ii.
The decimal representation of \(\frac{6}{1250}\) will terminate later how many places of decimal?
Solution:

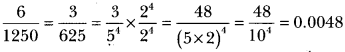
This representation will finish after four decimal places.

Question three.
If HCF of a and b is 12 and product of these numbers is 1800. Then what is LCM of these numbers?
Solution:
Product of 2 numbers = Production of their LCM and HCF
⇒ 1800 = 12 × LCM
⇒ LCM = \(\frac{1800}{12}\) = 150.

Costless Least Common Denominator calculator – Observe the LCD of two or more numbers step-by-step.

Question four.
What is the HCF of iii³ × 5 and 3ⁱⁱ × 5²?
Solution:
HCF of three³ × 5 and threeⁱⁱ × 5² = 3² × 5 = 45

Question v.
if a is an odd number, b is not divisible by iii and LCM of a and b is P, what is the LCM of 3a and 2b?
Solution:
6P

Question 6.
If P is prime then, what is the LCM of P, P^two, P³?
Solution:
P³

Question seven.
Two positive integers p and q can exist expressed as p = ab² and q = a^twob, a and b are prime numbers. What is the LCM of p and q?
Solution:
aⁱⁱh²

Question 8.
A number N when divided by fourteen gives the remainder 5. What is the remainder when the same
number is divided past 7?
Solution:
5, because 14 is multiple of 7.
Therefore, remainder in both cases are aforementioned.

Question 9.
Examine whether \(\frac{17}{30}\) is a terminating decimal or not.
Solution:

Since the denominator has 3 as its factor.
∴ \(\frac{17}{thirty}\) is a non4ermznatlng decimal.

Question 10.
What are the possible values of rest r, when a positive integer a is divided by 3?
Solution:
According to Euclid'southward partition lemma
a = 3q + r, where O r < three and r is an integer.
Therefore, the values of r can be 0, ane or 2.

Question 11.
A rational number in its decimal expansion is 1.7351. What tin yous say nigh the prime factors of q when this number is expressed in the form \(\frac{p}{q}\) ? Give reason.
Solution:
Every bit 1.7351 is a terminating decimal number, and so q must be of the form ii^m 5ⁿ, where in, n are natural numbers.

Question 12.
Without really performing the long division, find \(\frac{987}{10500}\) will have terminating or non.terminating repeating decimal expansion. Requite reason for your answer.
Solution:
\(\frac{987}{10500}\) = \(\frac{47}{500}\) and 500 = 2² × five³, so it has terminating decimal expansion.

Real Numbers Class 10 Actress Questions Brusque Answer Type 1

Question 1.
Can the number fourⁿ, due north be a natural number, end with the digit 0? Give reason.
Solution:
if iv^{due north} ends with 0, then information technology must have five as a factor. Only, (4)ⁿ = (ii²)^northward = 2²ⁿ i.due east., the only prime factor
of 4ⁿ is 2. Also, we know from the fundamental theorem of arithmetic that the prime number factorization of each number is unique.
∴ 4ⁿ can never end with 0.

Question ii.
Write whether the square of whatsoever positive integer can be of the form 3m + 2, where m is a natural number. Justify your reply.
Solution:
No, considering any positive integer can exist written every bit 3q, 3q + i, 3q + two, therefore, square will be
9q² = 3m, 9q² + 6q + 1 = iii(3q²+ 2q) + 1 = 3m + one,
9q² + 12q + 4 = three(3q²+ 4q + 1) + i = 3m + 1.

Question three.
Can ii numbers take eighteen as their HCF and 380 every bit their LCM? Give reason.
Solution:
No, considering hither HCF (18) does not divide LCM (380).

Question 4.
Write a rational number between √3 and √5.
Solution:
A rational number between √3 and √five is √iii.24 = 1.8 = \(\frac{18}{10}\) = \(\frac{9}{v}\)

Question 5.
The product of two consecutive integers is divisible by two. Is this statement truthful or false? Give reason.
Solution:
True, because n(north + 1) volition e'er be even, every bit ane out of the n or n+ one must exist even.

Question 6.
Explain why three × 5 × 7 + 7 is a blended number.
Solution:
iii × five × 7 + 7 = 7(3 × v + i) = 7 × 16, which has more than two factors.

Question 7.
What is the least number that is divisible by all the numbers from 1 to x?
Solution:
Required number = LCM of i, 2, three, … 10 = 2520

Question 8.
Find the sum \(0 . \overline{68}\) + \(0 . \overline{73}\).
Solution:

Question 9.
"The production of three sequent positive integers is divisible by 6". Is this statement true or false? Justify your answer.
Solution:
True, because n(north + 1) (due north + 2) will e'er be divisible by 6, as at least 1 of the factors will be divisible by 2 and at least one of the factors will be divisible by 3.

Real Numbers Class 10 Extra Questions Brusque Answer Blazon ii

Question i.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the aforementioned number of columns. What is the maximum number of columns in which they can march?
Solution:
For the maximum number of columns, we accept to find the HCF of 616 and 32.
At present, since 616 > 32, nosotros apply segmentation lemma to 616 and 32.
We have, 616 = 32 × 19 + 8
Here, remainder eight ≠ O. So, we again employ partition lemma to 32 and 8.
We have, 32 = viii × 4 + O
Here, balance is naught. So, HCF (616, 32) = 8
Hence, maximum number of columns is 8.

Question 2.
Find the LCM and HCF of 12, 15 and 21 by applying the prime factorisation method.
Solution:
The prime factors of 12, 15 and 21 are
12 2² × 3, 15 = 3 × v and 21 = 3 × seven
Therefore, the HCF of these integers is 3.
ii^two, 3¹, 5¹ and 7¹ and are the greatest powers involved in the prime number factors of 12, 15 and 21.
So, LCM (12, xv, 21) = 2² × 3ⁱ × 5^ane × 7¹ = 420.

Question 3.
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(1) 26 and 91 (2) 198 and 144
Solution:
(i) We have, 26 = two × 13 and 91 = seven × 13
Thus, LCM (26, 91) = 2 × vii × 13 = 182
HCF (26, 91) = 13
Now, LCM (26, 91) × HCF (26, 91) = 182 × 13 = 2366
and Product of the 2 numbers = 26 × 91 = 2366
Hence, LCM × HCF = Production of two numbers.

(two) 144 = 24 × 32 and 198 = 2 × 32 × 11
∴ LCM(198,144)2^iv × 3² × eleven = 1584
HCF(198, 144) = 2 × 3² = 18
Now, LCM (198, 144) × HCF (198, 144) = 1584 × 18 = 28512
and production of 198 and 144 = 28512
Thus, product of LCM (198, 144) and HCF (198, 144)
= Product of 198 and 144.

Question 4.
There is a circular path effectually a sports field. Sonia takes 18 minutes to drive 1 round of the field, while Ravi takes 12 minutes for the aforementioned. Suppose they both start from the same point and at the same time, and get in the same direction. Later on how many minutes will they run across again at the starting point?
Solution:
To detect the time after which they meet once again at the starting point, nosotros take to detect LCM of 18 and 12 minutes. We have

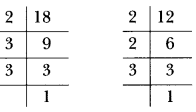
Therefore, LCM of 18 and 12 = 2² × 3² = 36
Then, they will meet over again at the starting point after 36 minutes.

Question 5.
Write down the decimal expansiwns of the post-obit numbers:
(i) \(\frac{35}{fifty}\) (two) \(\frac{xv}{1600}\)
Solution:
(i)

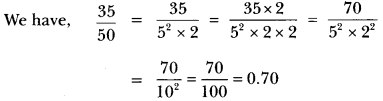
(ii)

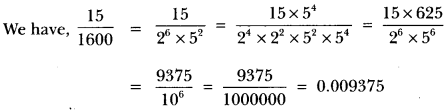
Question six.
Express the number \(0.iii \overline{178}\) in the form of rational number \(\frac{a}{b}\)
Solution:
Let x = \(0.3 \overline{178}\)
and then x = 0.3178178178 … … (1)
10x = 3.178178178 … …(two)
10000x = 3178.178178… …(iii)
On subtracting (ii) from (3), we get

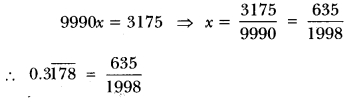
Question 7.
If n is an odd positive integer, show that (nⁱⁱ – ane) is divisible past 8.
Solution:
Nosotros know that an odd positive integer n is of the class (4q + 1) or (4 + 3) for some integer q.
Case – I When n = (4q + 1)
In this case north^two – ane = (4q + ane)²1 = 16q² + 8q = 8q(2q + 1)
which is clearly divisible by 8.

Case – 2 When n = (4q + iii)
In this example, we have
n2² = (4q + 3)^two – ane = 16q^two + 24q + viii = 8(2q²+ 3q + 1)
which is clearly divisible past 8.
Hence (n² – 1) is divisible past eight.

Question 8.
The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one
number is 280, so find the other number.
Solution:
Allow HCF of the numbers hex then co-ordinate to question LCM of the number will be 14x
And x + xiv = 600 ⇒ 15x = 600 ⇒ x = 40
And then HCF = 40 and LCM = xiv × 40 = 560
∵ LCM × HCF = Product of the numbers
560 × forty = 280 × Second number 2nd number = \(\frac{560 \times 40}{280}\) = 80
Then other number is 80

Question 9.
Observe the value of x, y and z in the given cistron tree. Tin can the value of 'x' be plant without finding the value of 'y' and 'z'? If yes, explicate.

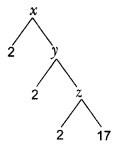
Solution:
z = two × 17 = 34; y = 34 × 2 = 68 and 10 = 2 × 68 = 136
Aye, value of x can exist found without finding value of y or z every bit
x = 2 × 2 × ii × 17 which arc prime 1tctors of x.

Question 10.
Show that any positive odd integer is of the form 6q + 1 or 6q + S or 6q + v where q is some integer.
Solution:
Let a he whatsoever positive odd integer and h = half-dozen. Then, by Euclid'south algorithm, a = 6q + r, for some
integer q ≥ O and O ≤ r < 6.
i.e., the possible remainders are 0, 1, two, 3, four, 5.
one'hus,a canbeoftheform6q,or6q + I,or6q + two,orßq + iii,ör6q + four,
or 6q + five, where q is some caliber.
Since a. is odd integer, and then a cannot be of the grade , or + 2, or 6q + 4, (since they are fifty-fifty).
Thus, a is of the form 6q + 1, 6q + three, or 6q + five, where q is some integer.
Hence, whatever odd positive integer is of the course 6q + one or 6q -1- 3 or 6q + 5, where q is sorne integer.

Question eleven.
The decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write information technology in the grade \(\frac{p}{q}\). What tin you say about the prime factors of q?
(i) 0.140140014000140000… (ii) \(0 . \overline{16}\)
Solution:
(i) We have, 0.140140014000140000… a non-terminating and non-repeating decimal expansion. So it is irrational. It cannot be written in the form of \(\frac{p}{q}\)

(ii) Nosotros accept, \(0 . \overline{xvi}\) a non-terminating but repeating decimal expansion. So it is rational.
Allow x = \(0 . \overline{16}\)
So, ten = 0.1616… (i)
100×16.1616… ..(ii)
On subtracting (i) from (two), nosotros get
100x – x = 16.1616 – 0.1616
⇒ 99x = 16 ⇒ ten = \(\frac{xvi}{99}\) = \(\frac{p}{q}\)
The denominator (q) has factors other than two or 5.

Real Numbers Class 10 Extra Questions Long Answer Type 1

Question 1.
Use Euclid's sectionalisation lemma to testify that the square of any positive integer is either of the course 3m or 3m + 1 for some integer one thousand.
Solution:
Let a be an arbitrary positive integer.
Then by Euclid'south partitioning algorithm, corresponding to the positive integers a and 3 in that location exist
non-negative integers q and r such that
a = 3q + r where 0 ≤ r <three
a² = 9q^two + 6qr + r² ….(i) 0 ≤ r <iii

Case – I: When r = 0 [putting in (i)]
a² = 9q^two = 3(3qⁱⁱ) = 3m where m = 3q²

Case – II: r = one
a^two = 9q^two+6q + 1 = 3(3q² + 2q)+ i = 3m + one where m = 3q² + 2q

Case – Iii: r = 2
aⁱⁱ = 9qⁱⁱ + 12 + 4 = three(3q² + 4q + one) + one = 3m + 1 where m = (3q² + 4q + 1)
Hence, foursquare of any positive integer is either of the course 3m or 3m + ane for some integer m.

Question ii.
Show that 1 and but one out of n, due north + 2, n + iv is divisible by three, where n is any positive integer.
Solution:
Allow q exist the quotient and r be the residuum when due north is divided by 3.
Therefore, n = 3q + r, where r = 0, 1, two
n = 3q or n = 3q + one or northward = 3q + 2
Instance (i) if n = 3q, then n is divisible by 3, n + ii and n +. four arc not divisible by iii.
Case (two) if 71 = 3q + 1 then n + 2 = 3q + iii = three(q + one), which is divisible by 3 and
north + 4 = 3q + v, which is not divisible by 3.
And so, only (northward + 2) is divisible by 3.
Example (iii) If northward = 3q + 2, then n + 2 = 3q + 4, which is not divisible by 3 and
(north + 4) = 3q + 6 = 3(q + 2), which is divisible by 3.
And so, merely (n + 4) is divisible by 3.
Hence one and merely one out of n, (n + 2), (n + 4), is divisible by 3.

Question 3.
Use Euclid's division algorithm to find the HCF of:
(i) 960and432
(ii) 4052 and 12576.
Solution:
(j) Since 960 > 432, we employ the division lemma to 960 and 432.
Nosotros have, 960 = 432 × ii + 96
Since the remainder 96 ≠ 0, and so nosotros apply the division lemma to 432 and 96.
We accept, 432 = 96 × iv + 48
Once again remainder 48 ≠ 0 so we once again apply division lemma to 96 and 48.
We take, 96 = 48 × 2 + O
The remainder has at present become zero. So our process stops.
Since the divisor at this phase is 48.
Hence, HOE of 960 and 432 is 48.
i.e., HCF (960, 432) = 4H

(two) Since 12576 > 4052, we apply the sectionalisation lemma to 12576 and 4052, to get
12576 = 4052 × 3 + 420
Since the remainder 420 ≠ 0, we utilize the partitioning lemma to 4052 and 420, to get
4052 = 420 × nine + 272
We consider the new divisor 420 and the new remainder 272, and apply the division lemma to become
420 = 272 × 1 + 148
We consider the new divisor 272 and the new remainder 148, and apply the sectionalisation lemma to get
272 = 148 × 1 + 124
We consider the new divisor 148 and the new remainder 124, and apply the sectionalization lemma to get
148 = 124 × ane + 24
We consider the new divisor 124 and the new residuum 24, and employ the division lemma to get
124 = 24 × five + 4
We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get
24 = 4 × 6 + O
The remainder has at present become zero, so our procedure stops. Since the divisor at this stage is four, the HCF of 12576 and 4052 is iv.

Question iv.
Using prime factorisation method, find the HCF and LCM of 30, 72 and 432. Also evidence that HCF × LCM ≠ Production of the iii numbers.
Solution:
Given members = 30, 72, 432 .
thirty = 2 × 3 × v; seven² = two³ × 3² and 432 = 2^four × iii^three
Here, ii' and 31 are the smallest powers of the mutual factors 2 and 3 respectively.
So, HCF (30, 72, 432) = ii¹ × three¹ = 2× 3 = half-dozen
Again, ii, 33 and 51 arc the greatest powers of the prime factors two, iii and v respectively.
And then, LCM (thirty, 72, 432) = 2⁴ × 3ⁱⁱⁱ × 5^ane = 2160
HCF × LCM = half-dozen × 2160 = 12960
Product of numbers = 30 × 72 × 432 = 933120 .
Therefore, HCF × LCM ≠ Product of the numbers.

Question v.
Show that √vii is an irrational number.
Solution:
Let us presume, to the contrary, that √7 is a rational number.
Then, at that place exist co-prime positive integers and such that
√7 = \(\frac{a}{b}\) , b ≠ 0
So, a = √seven b
Squaring both sides, we have
aⁱⁱ = 7b² …… (i)
⇒ 7 divides a² ⇒ 7 divides a
So, we can write
a = 7c (where c is an integer)
Putting the value of a = 7c in (i), we take
49cⁱⁱ = 7bⁱⁱ 7² = bⁱⁱ
It means 7 divides b^two and and so 7 divides b.
So, seven is a common factor of both a and b which is a contradiction.
So, our assumption that √7 is rational is wrong.
Hence, we conclude that √7 is an irrational number.

Question half dozen.
Bear witness that 5 – √iii is an irrational number.
Solution:
Let us assume that 5 – √three is rational.
So, five – √iii may be written as
five – √3 = \(\frac{p}{q}\), where p and q are integers, having no common cistron except ane and q ≠ 0.
⇒ 5 – \(\frac{p}{q}\) = √iii ⇒ √iii = \(\frac{5 q-p}{q}\)
Since \(\frac{v q-p}{q}\) is a rational number every bit p and q are integers.
∴ √three is also a rational number which is a contradiction.
Thus, our assumption is wrong.
Hence, 5 – √3 is an irrational number.

Question 7.
Using Euclid'due south division algorithm, find whether the pair of numbers 847,2160 are co-prime or not.
Solution:
Since 2160 > 847 nosotros apply the sectionalisation lemma to 2160 and 847
we have, 2160 847 × two + 466
Since residue 466 ≠ 0. So, nosotros apply the division lemma to 847 and 466
847 = 466 × ane+ 381
Again balance 381 ≠ 0. So we over again apply the partition lemma to 466 and 381.
466 = 381 × 1 + 85
Again remainder 85 ≠0. So, we again apply the division lemma to 381 and 85
381 = 85 × four + 41
Again remainder 41 ≠ 0. So, we again use the division lemma to 85 and 41.
85 = 41 × two + three
Once again remainder 3 ≠ 0. So, we over again apply the division lemma to 4 ane and three.
41 = 3 × 13 + 2
Over again residual ii ≠ 0. And then, we once more utilise the division lemma to 3 and two.
iii = 2 × 1 + ane
Again remainder 1 ≠ 0. So, we apply division lemma to 2 and 1
2 = i × two + 0
The remainder at present becomes O. And then, our procedure stops.
Since the divisor at this stage is 1.
Hence, HCF of 847 and 2160 is 1 and numbers are co-prime.

Question 8.
Cheque whether 6^{due north} can end with the digit O for any natural number n.
Solution:
If the number 6^north, for any n, were to terminate with the digit zero, then h would bc divisible by v. That is, the prime factorisation of 6^north would comprise the prime 5. But 6^north = (2 × 3)ⁿ = two^north × iiiⁿ And then the primes in factorisation of 6ⁿ are 2 and iii. So the uniqueness of the Cardinal Theorem of Arithmetics guarantees that (here are no other primes except ii and iii in the factorisation of 6ⁿ. And then there is no natural number due north for which 6" ends with digit nil.

Real Numbers Class 10 Extra Questions HOTS

Question ane.
Show that there is iw positive integer north for which \(\sqrt{north-1}\) + \(\sqrt{n+1}\) is rational.
Solution:
Permit there be a positive integer n for which \(\sqrt{north-1}\) + \(\sqrt{n+one}\) be rational number.

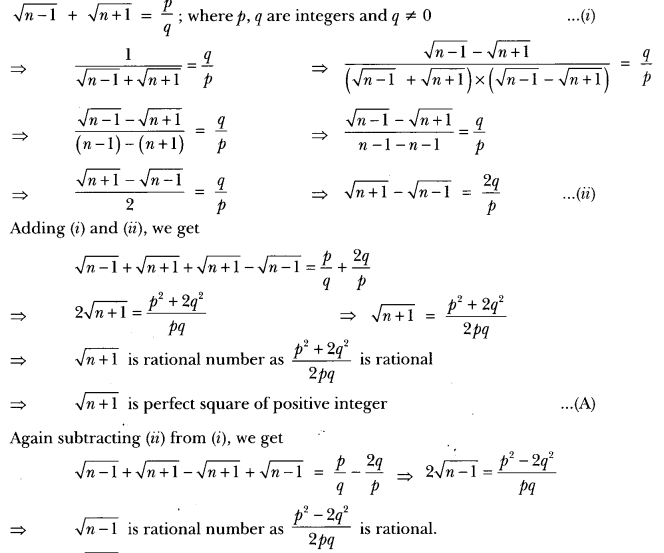
⇒ \(\sqrt{northward-1}\) is also perfect. square of positive integer From (A) and (B)
\(\sqrt{north+1}\) and \(\sqrt{n-1}\) are perfect squares of positive integer. It contradict the fact that two perfect
squares differ at least by 3.
Hence, at that place is no positive integer n for which\(\sqrt{north-one}\) + \(\sqrt{due north+1}\) is rational.

Question two.
Let a, b, e, chiliad be rational numbers such that k is not a perfect cube. if a + bk^1/2 + ck^ii/3 and then prove that a = b, c = 0.
Solution:


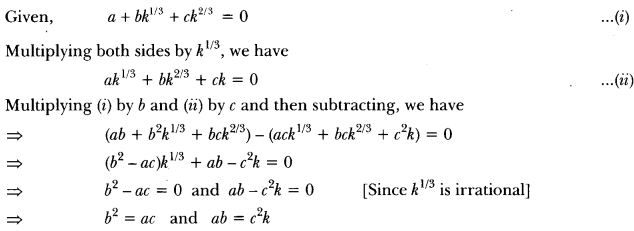
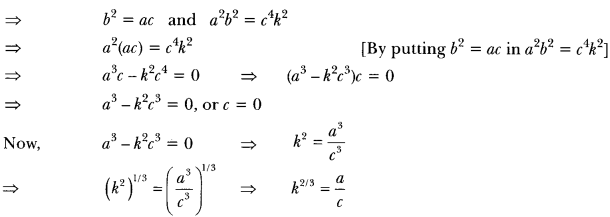
This is impossible as chiliad^ii/iii is irrational and \(\frac{a}{c}\) is rational.
∴ a³ – one thousand^twocⁱⁱⁱ ≠ 0
Hence, c = 0
Substituting c = 0 in b² – ac = 0, nosotros get b = 0
Substituting b = 0 and c = 0 in a + bk^1/iii + ck^ii/3= 0, nosotros get a = 0
Hence, a = b = c = 0
Question 3.
Observe the largest positive integer that will carve up 398, 436 and 542 leaving remainders vii, 11 and xv respectively.
Solution:
It is given that on dividing 398 by the required number, there is a remainder of 7. This means that 398 – 7 = 391 is exactly divisible by the required timber In other words, required number is a gene of 391.
Similarly, required positive integer is a Íctor of 436 – xi = 425 and 542 – 15 = 527
Clearly, the required number is the HCF of 391, 425 and 527.
Using the cistron tree, we get the prime factorisations of 391, 425 and 527 as follows:
391 = 17 × 23, 425 52 × 17 and 527 17 × 31
∴ HCF of 391, 425, and 527 is 17.
Hence, the required number = 17.

martingonded.blogspot.com

Source: https://www.learninsta.com/real-numbers-class-10-extra-questions/